论文原文：Large Language Models Are Zero-Shot Time Series Forecasters

摘要

通过将时间序列编码为一串数字，我们可以将时间序列预测视为文本中的下一个标记预测。在开发这种方法时，我们发现大型语言模型（如GPT-3和LLaMA-2）可以令人惊讶地在零样本外推时间序列，其性能可与或超过在下游任务上训练的专用时间序列模型的性能相媲美。为了提高性能，我们提出了一种有效地对时间序列数据进行标记化和将离散分布转换为高度灵活的连续值密度的方法。我们认为，语言模型在处理时间序列方面的成功源于其能够自然地表示多模态分布，结合了简单性和重复性的偏好，这与许多时间序列的显著特征（如重复的季节性趋势）相吻合。我们还展示了语言模型如何通过非数值文本自然地处理缺失数据，适应文本侧信息，并回答问题以帮助解释预测结果。 尽管我们发现增加模型大小通常会提高时间序列的性能，但我们发现由于数字的分词方式以及不良的不确定性校准，GPT-4的表现可能会比GPT-3差，这很可能是由于诸如RLHF等对齐干预的结果。

1. 引言

尽管与文本、音频或视频等其他序列建模问题相似，时间序列具有两个特别具有挑战性的属性。与通常具有一致的输入比例和采样率的视频或音频不同，聚合的时间序列数据集通常包含来自完全不同来源的序列，有时还会存在缺失值。此外，时间序列预测的常见应用，如天气或金融数据，需要从包含极少可能信息的观测中进行外推，使得准确的点预测几乎不可能，因此不确定性估计尤为重要。虽然大规模预训练已成为训练视觉和文本中的大型神经网络的关键要素，使性能能够直接与数据可用性相匹配，但在时间序列建模中通常不使用预训练，因为缺乏共识的无监督目标，并且大规模、连贯的预训练数据集不容易获取。因此，在流行的基准测试中，简单的时间序列方法（例如ARIMA（Box和Jenkins，1968）和线性模型（Zeng等，2022））通常优于深度学习方法（Hewamalage等）。[20], 2023).

在本文中，我们展示了大语言模型（LLM）如何自然地弥合传统方法的简单偏见与现代深度学习的复杂表示学习和生成能力之间的差距。特别地，我们引入了一种非常简单的方法，LLMTime。

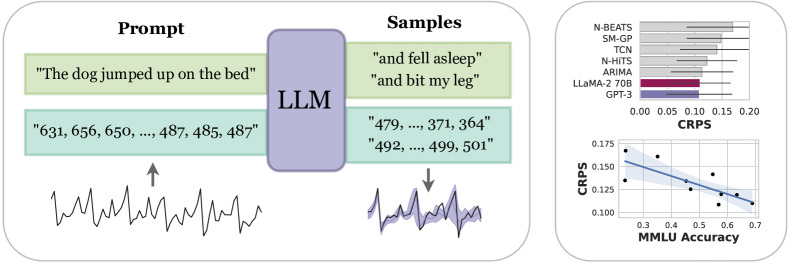
为了解决连续时间序列预测问题，我们提出了一种使用预训练LLMs的方法，如图1所示。在核心部分，该方法将时间序列表示为一串数字，并将时间序列预测视为文本中的下一个标记的预测，从而利用了强大的预训练模型和概率能力，例如似然度评估和采样。为了实现强大的性能，我们提出了两种技术：（1）将时间序列有效地编码为一串数字，（2）将LLMs的离散分布调整为能够建模复杂多模态分布的连续密度。使用这些技术，我们发现LLMTime可以在多种不同问题上超越或与专门设计的时间序列方法相匹配，而且无需对其他模型使用的下游数据进行任何微调即可实现。

LLMTime的zero-shot特性具有几个自然优势：(1) 它便于直接应用LLMs，消除了需要专门了解微调程序和大量计算资源的必要性，同时避免了访问专有源代码或LLM训练或微调的API的问题；(2) 它自然适用于数据有限的场景，其中训练或微调的信息很少；(3) 通过利用广泛预训练的LLMs的广泛模式外推能力，它避免了通常需要耗费大量时间、精力和领域专业知识来构建专用时间序列模型的问题。

为了理解LLMTime出色的性能起源，我们研究了LLMs对简单或重复序列的偏好（Goldblum等人，2023），并表明这些偏好实际上与时间序列的显著结构（如季节性）是相容的。除了这些偏好之外，LLMs还可以自然地适应缺失数据，并表达多模态分布，这对于时间序列尤其有用。我们还展示了LLMs如何实现吸引人的功能，例如通过提示提供额外的辅助信息，并查询LLM以解释其预测。

最后，除了具有广泛的预测性能之外，我们发现性能往往随着规模的增大而提高，而点预测的质量也随着不确定性表示的质量而提高。然而，我们还发现GPT-4的不确定性校准比GPT-3差，这可能是由于人类反馈强化学习等干预措施所致。

2. 背景

语言模型：语言模型是在一系列序列 $\mathcal{U} = {U_1, U_2, \dots, U_i, \dots, U_N}$ 上进行训练的，其中 $U_i = (u_1,u_2,\dots,u_j,\dots,u_{n_i})$ ，每个token $u_i$ 属于一个词汇表 $\mathcal{V}$。大型语言模型通常编码为自回归分布，其中每个token的概率仅依赖于序列中的前面的tokens $p_\theta\left( U_i\right) = \prod_{j=1}^{n_i} p_\theta\left(u_j \mid u_{0:j-1}\right)$。参数 $\theta$ 通过最大化整个数据集 ${p_\theta(\mathcal{U}) = \prod_{i=1}^N p_\theta(U_i)}$ 的概率来学习。每个语言模型都有一个关联的分词器，它将输入字符串分解为一系列 tokens，每个token属于 𝒱 。正确的分词非常重要，细节的微小变化可能会产生意想不到的显著影响。自回归语言模型最常见的分词方法是字节对编码（BPE），它将输入视为位串，并根据在训练语料库中出现的频率分配token，以便平均生成较短的token序列。从语言模型中进行采样通常从一个提示 $u_{0:k}$，并使用 $p_\theta\left(u_j \mid u_{0:j-1}\right)$进行预处理，例如通过温度缩放或核心采样（Holtzman等，2019）。

大语言模型：Brown 等人（2020）表明，增加语言模型的参数数量和训练数据大小会带来新的能力，例如零样本泛化，即模型可以在没有对任何特定任务的数据进行训练的情况下执行文本格式的任务。大型语言模型，例如 GPT-3（Brown 等人，2020）或 LLaMA-2（Touvron 等人，2023b），通过上下文学习实现这种泛化，它通过识别语言模型的提示中的模式，并通过下一个token的预测进行推断。许多作者推测，上下文学习是由语言模型对输入数据进行广泛压缩而产生的（Goldblum 等人，2023；Sutskever，2023；Delétang 等人，2023）。压缩有利于使用编程抽象在输入数据上操作的学习算法，例如无上下文文法（Allen-Zhu 和 Li，2023）或归纳头（Olsson 等人，2022），它们可以实现复制粘贴类型的操作，以生成具有高度结构化语法的样本。 在这项工作中，我们展示了LLMs的zero-shot泛化能力以及它们对可压缩模式的偏好不仅限于语言理解，还可以用于时间序列预测。

零样本泛化使得LLMs作为助手变得更加有用，人们借此创建了一些方法，用于将LLMs与人类的偏好和指令进行对齐，例如从人类反馈中进行强化学习（RLHF）（Ouyang等，2022）和指令调整（Wei等，2021）。虽然对于现代LLMs产品至关重要，但对齐方法也会显著影响底层模型的能力和校准（OpenAI，2023；Bubeck等，2023）。在这里，我们展示了这些方法也会影响预测能力。

时间序列数据：时间序列数据通常与语言建模数据具有相同的形式，都是一系列的序列 $U_i = (u_1,u_2,\dots,u_j,\dots,u_{n_i})$ ，但在时间序列中 $u_j$ 是数值型的。由于语言模型的构建是为了表示复杂的序列概率分布，因此从理论上讲，它们非常适合用于时间序列建模。然而，在实践中，语言模型受到了对数字进行分词的细节的限制。BPE（字节对编码）根据在训练数据中出现的频率压缩数字，因此数字可能被分解成令人尴尬的片段，这使得学习基本数值运算变得具有挑战性。因此，Touvron等人（2023a）设计了LLaMA分词器，将数字映射为单个digits，这可以显著提高数学能力，小型LLaMA模型的性能超过了GPT-4（Liu和Low，2023）。

将语言模型应用于时间序列数据的另一个挑战是适当的评估。通常使用的是均方绝对误差（MAE），但它忽略了预测中的不确定性，这对于随机数据限制很大（Hewamalage等，2023; Benton等，2022）。连续排名概率分数（CRPS）捕捉了分布特性，并且可以比较生成样本而不是似然的模型。对于单个预测，CRPS分数定义为针对估计的累积分布函数（CDF）的$\hat{F}$ ，其中$ \text{CRPS}(\hat{F},y) = \int_{\mathbb{R}} \left(\hat{F}(z) - \mathbb{I}_{(z - y) > 0}\right)^2 dz, $ 是通过采样预测产生的经验CDF， $\hat{F}(z)$ 是指示函数。虽然CRPS相对于MAE是一种改进，但它也忽略了数据中的关键结构，例如时间步之间的相关性。幸运的是，语言模型可以为完整的时间序列数据分配似然，我们展示了如何对LLM的离散似然进行小的修改，从而得到一个对模型比较有用的连续密度。

时间序列的语言模型：一些作者已经探索使用预训练的语言模型编码器作为时间序列模型的初始化工具。例如，Zhou等人（2023年）提出了FPT，它对BERT编码器进行微调以进行时间序列预测。同样，Zhang等人（2023年）引入了Meta-Transformer，这是一个用于对非文本模态（包括时间序列）进行语言模型微调的框架。少数几篇论文探索了在没有微调的情况下使用LLMs作为预测器的情况。我们所知道的唯一方法是PromptCast（Xue和Salim，2023年），它将预测视为带提示的问答过程。

我们的工作：与利用LLM骨干的方法不同，我们的方法完全是zero-shot的，不需要微调。与PromptCast不同，我们展示了如果我们仔细预处理数值本身，LLMs可以直接用作预测器，而不需要任何额外的文本或提示工程。我们的方法仅仅依赖于LLM在一般序列中外推模式的能力，而不依赖于英语或任何其他语言的特定内容。超越以往的工作，我们还培养了大型语言模型的概率性质以及它们捕捉高度随机时间序列的不确定性的能力。

3. LLMTime：使用语言模型进行预测

使用大语言模型进行预测相对来说步骤较少。一旦将数值处理成字符串，使用语言模型进行预测就遵循标准的采样过程。然而，正如我们接下来所展示的，正确的预处理并不总是直观的，但却非常重要，而处理不当可能导致无法使用的预测结果。

Tokenization：Tokenization特别重要，因为它直接影响到 tokenized 序列中模式的形成方式以及语言模型可以学习的操作类型。不幸的是，常见的tokenization方法如BPE往往会将一个数字(number)分成不与digits对齐的token，这可能会使算术运算变得更加困难（Liu和Low，2023）。例如，数字 42235630 在GPT-3的标记器中被标记为 [422,35,630] ，即使只改变一个数字，也可能导致完全不同的tokenization结果。相比之下，在许多新的开源LLMs（例如LLaMA（Touvron等，2023a））中，默认情况下将数字标记为单个数字。为了解决GPT模型的标记化问题，我们使用空格将数字的每个数字分开，以强制对每个数字进行单独的tokenization，并使用逗号（"，"）将时间序列中的每个时间步骤分开。由于在给定固定精度的情况下，小数点是多余的，我们在编码中去掉它们以节省上下文长度。因此，例如，在具有 2 位精度的情况下，我们在将时间序列输入标记器之前进行以下预处理：

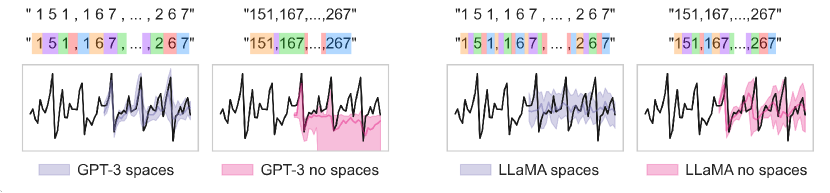
在图2中，我们展示了这种编码方式的额外空格对于GPT模型是有帮助的，可以防止模型在采样过程中输出异常的标记而偏离正常情况。对于LLaMA模型来说，由于其对数字的独特分词方式，额外的空格则产生了相反的效果。每个数字和空格已经被分配了自己的标记，空格标记成为了干扰输入，增加了序列长度但没有简化序列的结构，可能使得序列对于模型来说是超出分布范围的。

重新缩放：为了避免在输入非常大的情况下浪费标记，我们将值缩小，使得重新缩放的时间序列值的 $\alpha$ 百分位为 1 。我们避免使用最大值进行缩放，以便LLM可以看到一些数字位数发生变化的示例（ $1-\alpha$），并在其输出中重现此行为以产生比其所见过的更大的值。我们还尝试使用基于输入数据的百分位数计算的偏移量 $\beta$ ，并通过验证对数似然度来调整这两个参数（详见附录A）。

采样/预测：为了进行预测，从LLM中抽取多个样本（例如20个），并使用每个时间步骤的样本统计数据构建一个点估计（例如中位数）或概率预测（例如分位数）。为了控制采样，我们使用温度缩放、logit偏差和核心采样（附录C）。

连续似然性：对于建模数字序列来说，除了生成良好的样本之外，还有其他好处。在基数为 $B$ 的情况下，小数点后的 $n$ 位数字序列对应于 $B^n$ 个可能的区间（图3），每个区间的宽度为 $B^{-n}$ 。由于每个分布 \(p(u_j \mid u_{0:j-1}; \theta)\) 都是可能数字的softmax函数，我们可以将每个单独数字的分布视为分层softmax（Mnih和Hinton，2008），其中 \(p(u_1, ..., u_n)= p(u_n \mid u_{n-1}, ..., u_0) \, p(u_1 \mid u_0) \, p(u_0)\) 。尽管语言模型的概率分布是离散的，但我们可以通过在每个区间中放置均匀分布来轻松地将其调整为连续密度。用索引 $k \in \mathbb{N}$ 枚举模型可以产生的所有可数无穷数字(因为模型可以在小数点前输出任意数量的数字),每个概率为 $p_k$，我们可以将分布写成不相交均匀分布在区间$p(x) = \sum_{k \in \mathbb{N}} p_k U_k(x)$上的混合，其中 $U_k(x) = B^n\mathbb{I}_{x\in [B^{-n}k,B^{-n}(k+1))}$。因此,如果给定的数据点在区间 $k$ 中，其连续对数似然度为 $log p(x)=\log p_k + n\log B$。最后,为了获得原始输入空间中的似然度$log p(z)$，我们添加一个变量变换因子 \(log \vert\tfrac{dx}{dz}\vert,\) 其中 $z \mapsto x=s(z)$ 是预处理中的缩放操作。因此，我们的构造方式使得可以使用离散的数字标记来表示灵活且高分辨率的连续分布，尽管存在指数级数量的区间和指数级小的区间宽度，但其效率令人惊讶地高。

语言模型作为灵活的分布：语言模型可以表达数值的灵活分布，这个事实对于时间序列数据来说至关重要。不确定性量化对于预测至关重要，而表示时间序列中的不确定性的典型方法可能会受到错误规定的限制。例如，创建概率预测的常见方法之一是拟合高斯或拉普拉斯观测模型。当底层数据分布是多峰的时候，这两个模型都会表现不佳。高斯混合模型（GMMs）等方法可以解决多峰性问题，但会引入优化和模型选择方面的额外挑战。我们通过在各种一维分布上训练一个小型自回归模型来展示语言模型是一个被低估的解决方案，如图3（右侧）所示。这些分布来自指数随机变量、均匀分布和学生t分布的混合，以及基于MonthlyMilk数据集上ARIMA模型的时间序列预测残差的重尾分布（Herzen等人，2022）。 [20] 我们通过计算Wasserstein距离来定量评估这些拟合结果，并与拉普拉斯观测模型、使用期望最大化训练的高斯混合模型以及对数据进行平坦分箱的逻辑回归进行比较（使用调整后的区间大小）。每个模型仅使用分布中的 200 个样本进行训练。结果表明，十进制自回归语言模型（"Decimal AR"）表现非常出色，能够处理非对称、多峰和重尾分布，这些是时间序列数据的典型多样性类型之一。

7. 讨论

我们已经证明，大语言模型可以通过将数值编码为文本的方式用作预训练的时间序列预测器。与其他"基础"模型一样，预训练赋予了模型对可泛化模式的有用偏置，这些偏置原本需要通过架构设计来工程化地嵌入模型中[21]，并且能够随着基础预训练模型的改进自然地扩展性能。由于LLM预测器是在语言上训练的，它们还具备非常规的能力，比如问答功能。更广泛地说，将时间序列预测框架化为自然语言生成可以被视为在单一大型强大模型中统一更多能力的又一步，在这种模型中，理解可以在多个任务和模态之间共享。

此外，零样本预测能够在不需要大量计算资源、领域专业知识或大量下游训练数据点的情况下实现广泛令人信服的性能。

虽然LLM预测器受益于预训练transformer的优势，但它们也继承了其弱点，包括有限的上下文窗口。虽然许多单变量时间序列问题可以舒适地适应日益增大的上下文窗口，但多变量问题构成了更大的挑战。最近在将LLM上下文窗口扩展到10-100K个token方面有了几项进展[36, 4, 5, 1]。将这些进展与时间序列预测相结合是未来研究的一个特别令人兴奋的方向。

使用当前LLM架构的另一个潜在挑战可能是它们在算术以及执行递归和组合操作方面的弱点，这可能对特别具有挑战性的时间序列构成限制。另一方面，许多时间序列并不需要精确的算术。理解这种情况的程度，以及放宽这一限制，也是未来研究的一个有前景的方向。

除了任何限制之外，研究在时间序列上微调LLM的有效程序也将是很有前景的。我们希望将LLM研究与时间序列预测相结合能为两个社区带来益处。